Hasta
ahora se ha considerado que la corriente eléctrica se desplaza desde
el polo
positivo del generador al negativo (la corriente electrónica o real
lo hace al revés: los electrones se ven repelidos por el negativo
y atraídos por el positivo).
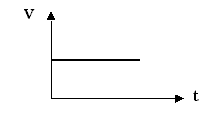
Fig.1 : Corriente continua
En una gráfica en la que en el eje horizontal se expresa el tiempo y
en el vertical la tensión en cada instante, la representación
de este tipo de corriente, que llamaremos CORRIENTE CONTINUA, es el de la figura
1, si el valor de la tensión es constante durante todo el tiempo y...
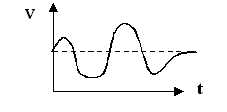
Fig.2 : Corriente continua variable
...la de la figura 2 si dicho valor varía a lo largo del tiempo (pero
nunca se hace negativa).
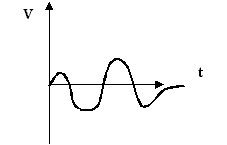
Fig.3 : Corriente alterna
Ahora bien, existen generadores en los que la polaridad está constantemente
cambiando de signo, por lo que el sentido de la corriente es uno durante un
intervalo de tiempo, y de sentido contrario en el intervalo siguiente.
Obsérvese que siempre existe paso de corriente; lo que varia constantemente
es el signo (el sentido) de ésta.
Naturalmente, para cambiar
de un sentido a otro, es preciso que pase por cero, por lo que el valor
de la tensión no será el mismo en todos los instantes. A
este tipo de corriente se le llama CORRIENTE ALTERNA, y, por el mismo motivo,
se habla de TENSIÓN ALTERNA. La figura 3 muestra un ejemplo de corriente alterna. La
corriente continua se abrevia con las letras C.C. (Corriente Continua) o D.C. (Direct Current), y la alterna, por C.A. (Corriente Alterna) o A.C. (Alternated
Current).
FUNCIONES PERIÓDICAS
El
caso más importante de corrientes alternas son las llamadas corrientes
alternas periódicas: son aquellas
en las que los valores se repiten cada cierto tiempo. El tiempo que tarda
en repetirse un valor se llama PERIODO
de la corriente, se expresa en unidades de tiempo y se representa por la
letra T.
En las figuras se muestran varios tipos de corrientes alternas periódicas.
Si en el eje horizontal se ha representado el tiempo, el periodo es el intervalo
que hay entre dos puntos consecutivos del mismo valor.
<-periodo->
Fig.1 : Corriente rectangular
Al máximo valor, se le llama precisamente, VALOR MÁXIMO, o VALOR DE
PICO o VALOR DE CRESTA, o AMPLITUD.
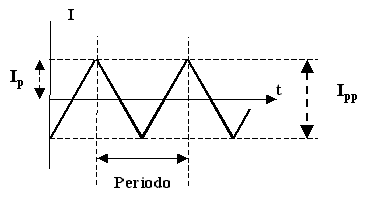
Fig.2 : Corriente triangular
El punto en que toma el valor máximo se llama CRESTA o PICO.
El punto en que toma el valor mínimo es el VIENTRE o VALLE.
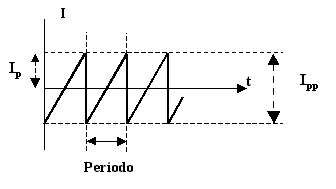
Fig.3 : Corriente en diente de sierra
Los puntos en los que toma el valor cero se les llama NODOS o CEROS.
La forma más cómoda de medir el periodo es entre picos, o valles,
o nodos consecutivos.
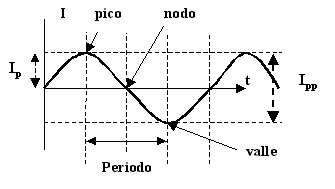
Fig.4 : Corriente sinusoidal
La diferencia entre un pico y un valle da el VALOR DE PICO A PICO que, naturalmente,
será el doble del valor de pico.
El valor de la corriente en cada instante es el VALOR INSTANTANEO.
el número de alternancias o ciclos que describe la corriente en un segundo
se le llama FRECUENCIA y se expresa en c/s (ciclos por segundo) o HERTZIOS (Hz).
Los múltiplos más usuales del hertzio son:
-
KILOHERTZIO (KHz.) = 103 Hz. (1.000 Hz)
-
MEGAHERTZIO (KHz.) = 106 Hz. (1.000.000 Hz)
-
GIGAHERTZIO (KHz.) = 109 Hz. (1.000.000.000 Hz)
La frecuencia resulta ser la inversa del período:
f = 1/T
CORRIENTE SINUSOIDAL
La más importante de las corrientes alternas periódicas es la
llamada corriente sinusoidal o senoidal, porque es la única capaz de pasar a
través de resistencias, boninas y condensadores sin deformarse. Puede
demostrarse que cualquier otra forma de onda se puede construir a partir de una
suma de ondas sinusoidales de determinadas frecuencias. Se llama sinusoidal
porque sigue la forma de la función matemática SENO. Que es la representada en
la figura.
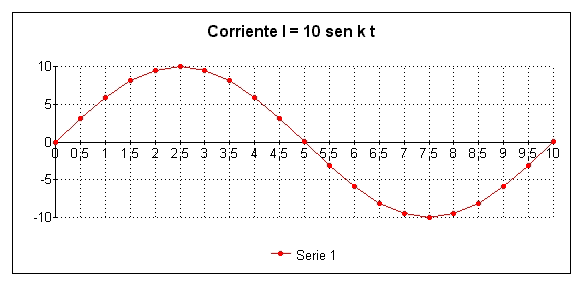
Figura 1
Esta función
es (si se trata de tensiones): vi = Vp sen kto bien (si se trata de corrientes)
ii = Ip sen ktdonde: vi es el valor instantáneo de la tensión,
es decir, el valor en un determinado instante t.
-
ii es el valor instantáneo de la corriente, es decir, el valor en
un determinado instante t.
-
Vp es el valor de pico de la tensión, también llamado amplitud
de la tensión
-
Ip es el valor de pico de la corriente, también llamado amplitud
de la corriente
-
k es una constante propia de la corriente de que se trate, relacionada con la
frecuencia, y cuya explicación se verá más adelante.
-
t es el tiempo expresado en segundos ( para cada instante t la tensión
tendrá un valor)
EJEMPLO: Sea una corriente de amplitud 10 A. y k = 628. Calcular los valores
instantáneos al cabo de 1,5 ms., 2,5 ms., y 7,5 ms.
-
Comprueba los datos calculados por tí con los de la tabla que sigue
más abajo, donde:
-
la primera columna está el tiempo ( t ) en ms.
-
la segunda columna está calculado el producto de la constante k
por el tiempo t. ( k t ).
-
Y la tercera columna se a multiplicado la amplitud de 10 por el sen de
kt.
La tabla I de valores obtenida es con la que se ha dibujado la señal de
la figura 1.
| Tiempo (milisegundos) |
kt |
I = 10 sen kt |
| 0 |
0.00 |
0.0000 |
| 0.5 |
314.16 |
3.0902 |
| 1 |
628.32 |
5.8779 |
| 1.5 |
942.48 |
8.0902 |
| 2 |
1256.64 |
9.5106 |
| 2.5 |
1570.80 |
10.000 |
| 3 |
1884.96 |
9.5106 |
| 3.5 |
2199.11 |
8.0902 |
| 4 |
2513.27 |
5.8779 |
| 4.5 |
2827.43 |
3.0902 |
| 5 |
3141.59 |
-0.0000 |
| 5.5 |
3455.75 |
-3.0902 |
| 6 |
3769.91 |
-5.8779 |
| 6.5 |
4084.07 |
-8.0902 |
| 7 |
4398.23 |
-9.5106 |
| 7.5 |
4712.39 |
-10.000 |
| 8 |
5026.55 |
-9.5106 |
| 8.5 |
5340.71 |
-8.0902 |
| 9 |
5654.87 |
-5.8779 |
| 9.5 |
5969.03 |
-3.0902 |
| 10 |
6283.19 |
0.0000 |
RELACIÓN ENTRE EL MOVIMIENTO SINUSOIDAL Y EL CIRCULAR
CONCEPTO
DE VELOCIDAD ANGULAR
La velocidad se expresa como la relación que existe entre el espacio recorrido
y el tiempo empleado en dicho recorrido.
Si el espacio recorrido es e y el tiempo empleado en recorrerlo es t diremos que
la velocidad v = e / t
Si usted recorre con su vehículo una distancia de 144 Km. en 2 horas, podemos
decir que su velocidad (media) es de
v = 144 / 2 = 72 Km./h.
Del mismo modo, en un movimiento circular, es decir, en aquel cuya trayectoria
es una circunferencia, se puede definir de otra manera la velocidad.
Ahora nos interesa, más que el camino recorrido, el ángulo que
ha descrito nuestro movimiento durante un tiempo determinado. Y así diremos
que si nuestro móvil se traslada a lo largo de la circunferencia un ángulo
de 70º en 2 segundos diremos que se ha movido con una velocidad de 70/2
= 35º en un segundo.
Esta nueva manera de expresar la velocidad se denomina VELOCIDAD ANGULAR. La
velocidad angular nos expresa la relación que existe entre el ángulo
recorrido por nuestro móvil y el tiempo empleado en recorrer dicho ángulo.
Dado que la unidad natural del ángulo es el RADIAN (La circunferencia tiene
2 p radianes). La velocidad angular se expresará en RADIANES POR
SEGUNDO (Rad/seg.).La velocidad angular, también llamada PULSACIÓN o FRECUENCIA
ANGULAR, se representa por la letra griega w (omega). Entonces , si un móvil
lleva una velocidad angular w ( por ejemplo, 4 rad/seg.), al cabo de un tiempo
t ( por ejemplo, 2 segundos), habrá descrito un ángulo (f):
que será igual al producto de la velocidad angular w por el tiempo t:f
= w t = 4 . 2 = 8 radianes
MOVIMIENTO
CIRCULAR Fijaros que al moverse el punto A a lo largo de la circunferencia, proyecta una
sombra (roja en la figura) de longitud OX
Si llamamos a al ángulo que forman la línea OA con la línea
OX se define el coseno del ángulo a como el cociente entre la distancia
OX y la distancia OA:
cos a = OX / OA
Por lo que podemos decir que OX = OA cosaEs decir que la proyección
del punto A es igual, al producto de OA por el coseno del ángulo que forma
con la horizontal. En la figura de abajo vemos que es la distancia del punto al
eje vertical (de color rojo en la figura) y marcada con una flecha en azul.
T es el tiempo que tarda el punto en recorrer la circunferencia, a este tiempo
le llamaremos periodo.
Si el punto A se mueve a lo largo de la circunferencia, observamos que:
Hemos dividido la parte superior de la circunferencia en 12 partes y para cada
punto la distancia al eje vertical, la hemos llevado a la parte inferior, y uniendo
los puntos obtenemos la curva del coseno.
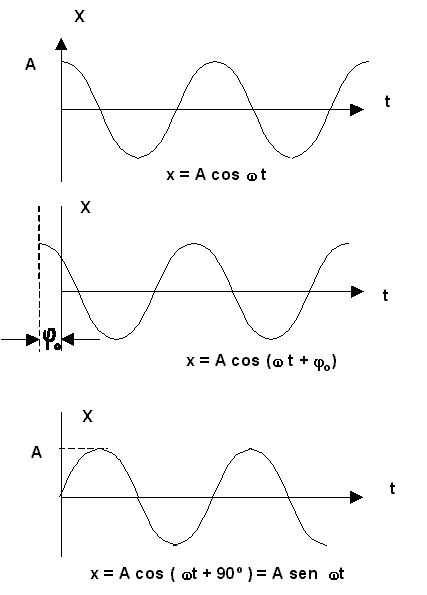
EL MOVIMIENTO SINUSOIDAL ES LA PROYECCIÓN DEL MOVIMIENTO
CIRCULAR
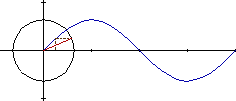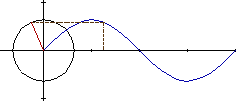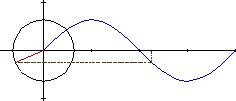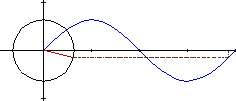
Resumiendo lo dicho:
Veamos el radio de amplitud A de la figura, que suponemos que
inicialmente forma
un ángulo j0 con la horizontal y que en cierto momento comienza a
girar con una velocidad w.
Al cabo de t segundos, se habrá desplazado un ángulo w t, por lo
que se encontrará formando un angulo f con la horizontal de valor j0 +
wt. La proyección en cada instante del extremo del radio sobre el eje horizontal
valdrá : x = cos (wt + j0 )
Sobre el movimiento circular (periódico) se definirán unos conceptos
que serán de aplicación en el movimiento sinusoidal: w =
PULSACIÓN: La pulsación del movimiento sinusoidal equivale a la velocidad angular
del movimiento circular. Se expresará, por tanto, en radianes por segundo.-
(Recordar que una circunferencia tiene 2 p radianes).
-
T = PERIODO: es el tiempo que tarda el radio en describir una vuelta completa,
que es, a su vez, el tiempo que tarda en repetir su valor.
-
f = FRECUENCIA : Es el número de vueltas por segundo y, por tanto, el
número de periodos por segundo.- (Su valor es la inversa de dicho periodo).
-
j0 = FASE : Es el ángulo inicial formado por el radio antes de empezar
a contar el tiempo. En el movimiento sinusoidal representa el desplazamiento
del eje vertical respecto del comienzo de la sinusoide.
-
A = AMPLITUD o VALOR MAXIMO de la sinusoide: Es el valor del radio en
el movimiento circular.
-
x(t) = VALOR INSTANTÁNEO. Es el valor de la sinusoide en cada instante. En el
movimiento circular es la proyección del radio sobre el eje horizontal.
Así pues, hay una relación
entre frecuencia, periodo y pulsación. En efecto:
Si para describir una vuelta se necesitan T segundos (por
ejemplo T = 0,5 seg.).
¿Cuántas vueltas describirá en 1 segundo?.
Lógicamente 2 vueltas.
Es decir
f = 1 / T o lo que es lo mismo T = 1 / f
Cada circunferencia tiene como ya se ha dicho 2 p radianes. Por lo tanto si se
describen f vueltas por segundo (por ejemplo 2 vueltas por segundo) equivale
a decir que la velocidad angular es de 2 p . 2 radianes por segundo es decir 4
p rad /s. w = 2 p f = 2 p / T La frecuencia resulta ser la inversa del período.
VALOR MEDIO Y VALOR EFICAZ
VALOR
MEDIO
Se llama valor medio de una tensión (o corriente) alterna a la media aritmética
de todos los valores instantáneos de tensión ( o corriente), medidos
en un cierto intervalo de tiempo.
En una corriente alterna sinusoidal, el valor medio durante un período
es nulo: en efecto, los valores positivos se compensan con los negativos. Vm
= 0. 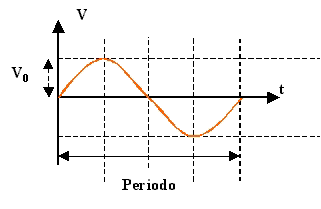
En cambio, durante medio periodo, el valor medio es 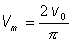 siendo
V0 el valor máximo. siendo
V0 el valor máximo.
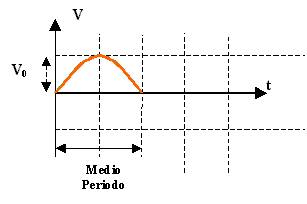 VALOR EFICAZ Se llama valor eficaz
de una corriente alterna, al valor que tendría una corriente continua que
produjera la misma potencia que dicha corriente alterna, al aplicarla sobre una
misma resistencia.
Es decir, se conoce el valor máximo de una corriente alterna (I0).
Se aplica ésta sobre una cierta resistencia y se mide la potencia producida
sobre ella.
A continuación, se busca un valor de corriente continua que produzca
la misma potencia sobre esa misma resistencia. A este último valor, se
le llama valor eficaz de la primera corriente (la alterna).
Para una señal sinusoidal, el valor eficaz de la tensión es:
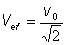 y del mismo modo para la corriente y del mismo modo para la corriente
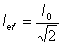 la potencia eficaz resultará
ser: la potencia eficaz resultará
ser:
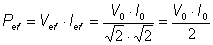
Es decir que es la mitad de la potencia máxima (o potencia de pico).
La tensión o la potencia eficaz, se nombran muchas veces por las letras
RMS. O sea, el decir 10 VRMS ó 15 WRMS sifnificarán 10 voltios eficaces
ó 15 watios eficaces, respectivamente. REPRESENTACIÓN VECTORIAL Introducción Una forma muy cómoda de representar gráficamente
las tensiones y corrientes alternas es la llamada vectorial.
Para ello se debe tener en cuenta que, en un determinado circuito, la frecuencia,
y, por tanto, la pulsación, será la misma en todos los puntos
del circuito.
Lo único verdaderamente importante es la fase relativa entre
cada tensión o cada corriente.
De este modo, se asigna fase cero a una determinada tensión o corriente,
y las demás se representan con su fase relativa a ésta.
Cada corriente o cada tensión se representa pues, por medio de un vector,
(una flecha con origen en el origen de coordenadas) formando un ángulo
con la horizontal igual a su fase, y con una magnitud (su longitud) igual a
su valor eficaz o de pico, como se prefiera. Componentes de un vector Breve repaso
de trigonometría:
Recordemos que en un triángulo rectángulo como el de la figura siguiente
se denomina hipotenusa al lado opuesto al ángulo recto (un ángulo
recto = 90º) y catetos a los otros dos lados.
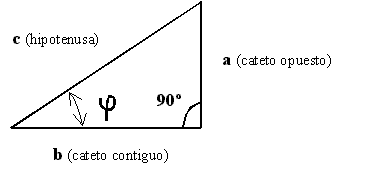
 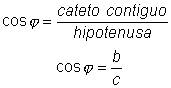 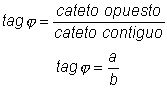
Si j es el ángulo formado entre el cateto b y la hipotenusa c, se llama seno del ángulo j( senj) al cociente entre el cateto opuesto
(a) y la hipotenusa (c). Y se escribe: se llama coseno del ángulo
j( cosj) al cociente entre el cateto contiguo (b) y la hipotenusa (c). Y se escribe: se llama tangente del ángulo
j( tagj) al cociente entre el cateto opuesto (a) y el cateto contiguo (b). Y se
escribe: Así pues, si tenemos
un vector, del que conocemos su módulo V (también llamado amplitud) y su fase j, podremos descomponerlo
en dos componentes, una horizontal y otra vertical, que llamaremos Vx y Vy; como
se indica en la figura siguiente:
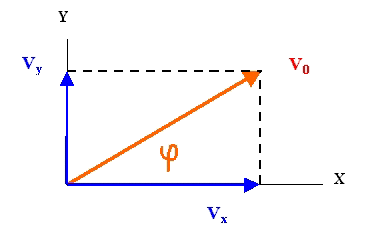
y por el repaso de trigonometría sabemos que podemos poner lo siguiente,
que:
La componente horizontal vale: 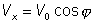 y
la componente vertical: y
la componente vertical: 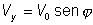
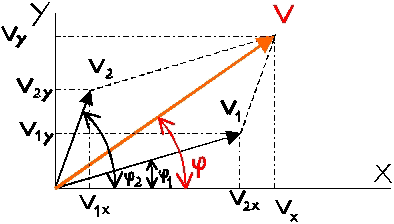
SUMA DE VECTORES
Se define la suma geométrica de dos vectores como indica la
figura:
¿Cómo se halla?
Por
el extremo de uno de ellos (V1) se traza la paralela al otro y por
el extremo del segundo (V2) se traza la paralela al primero; de esta
manera se ha definido un paralelogramo, cuya diagonal se llamará vector
suma ( V ) de los dos primeros vectores.
Para
realizar la suma matemáticamente (o numéricamente), de los
vectores V1 y V2 se calculan sus proyecciones sobre el eje de las X de
cada uno de ellos.
Y
así tendremos que el vector V1 proyectado sobre el
eje X obtendremos lo que llamaremos componente V1x y sobre
el eje de las Y que llamaremos componente V1y
V1x = V1 cos j1
V1y = V1 sen j1Y haciendo lo mismo con el vector V2 tendremos que el vector
V2 proyectado sobre el eje X obtendremos lo que llamaremos componente V2x y sobre
el eje de las Y que llamaremos componente V2y V2x = V2 cos j2
V2y = V2 sen j2El vector resultante V tendrá también dos componentes,
su proyección sobre el eje las X será la suma de las proyecciones,
también sobre el eje de las X de los vectores V1 y V2, es decir que: Vx=
V1x + V2xy su proyección sobre el eje las Y será la suma de las
proyecciones, también sobre el eje de las Y de los vectores V1 y V2, es
decir que: Vy = V1y + V2y Conocidas pues, las dos componentes del vector V (Vx,
Vy), se puede calcular V, por medio de: 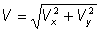 (Según el Teorema de Pitágoras)
(Según el Teorema de Pitágoras)
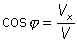 (De la definición de coseno)
(De la definición de coseno)
SUMA
DE VARIOS VECTORES Para
sumar varios vectores, se suman primeramente dos de ellos; el resultado
de esta operación con el siguiente, y así sucesivamente. RESTA
DE VECTORES Para
hacer la operación V1 - V2, se halla primeramente el
opuesto de V2 y después se suma éste con V1. Hay que tener
en cuenta que el opuesto de un vector es el mismo vector girado 180º. 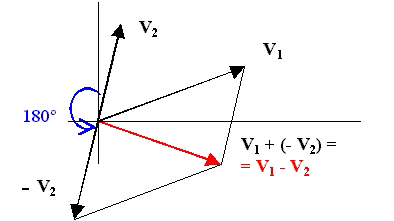
PRODUCTO Y COCIENTE DE VECTORES Para
multiplicar dos vectores, se multiplican sus módulos y se suman
sus fases.
Para
dividir dos vectores, se dividen sus módulos y se restan sus fases. |















