Las cargas en los conductores pueden moverse con cierta libertad. La corriente eléctrica constituye un movimiento continuado de las cargas libres. La cantidad de carga que circula por un conductor en la unidad de tiempo es la intensidad de corriente. Los responsables de mantener la corriente en un circuito eléctrico son los generadores eléctricos, los cuales suministran al circuito la energía precisa para ello. Dos leyes de naturaleza experimental descubiertas por Ohm y Joule respectivamente aportan algunas relaciones que facilitan el estudio científico de la corriente eléctrica.

La característica esencial de los conductores, sean éstos sólidos, líquidos o gaseosos, consiste en que disponen de partículas cargadas que pueden moverse con bastante libertad bajo la acción de campos eléctricos. Cuando un conductor descargado se pone en contacto con un cuerpo cargado se produce un desplazamiento de la carga del uno a otro por efecto de las fuerzas eléctricas. Si ambos están aislados, el movimiento de las cargas libres durará unos instantes entre tanto el sistema de cargas encuentra una configuración de equilibrio en la cual las fuerzas eléctricas que se ejercen sobre cada una de las cargas se compensan mutuamente. Esto es lo que sucede cuando un hilo metálico se conecta por uno de sus extremos a uno solo de los bornes de una pila. Sin embargo, cuando se conecta el otro extremo del conductor al segundo borne, se produce un movimiento continuado de cargas en el conductor. Se tiene en tal caso una corriente eléctrica. La parte de la física que se ocupa del estudio de este tipo de movimiento de las cargas eléctricas a través de un conductor recibe el nombre de electrocinética.

Globo de plasma que modeliza el ojo de la tormenta. En los globos de plasma se aplican voltajes de 3 kV a 8 kV y frecuencias de 20 kHz a 50 kHz entre el centro del globo y la capa exterior en contacto con la tierra.

CORRIENTE ELÉCTRICA

Movimiento de cargas y corriente eléctrica

La presencia de un campo eléctrico permanente en el seno de un conductor es la causa del movimiento continuado de las cargas libres. En términos de potencial puede decirse que para que se mantenga una corriente eléctrica es necesario que exista una diferencia de potencial constante entre los extremos del conductor. Si ésta disminuye por efecto de la circulación de las cargas, el campo eléctrico llega a hacerse nulo y cesa el movimiento. Esta es la situación que corresponde a esos desplazamientos de carga que se producen cuando un conductor aislado se carga o descarga eléctricamente.

Debido a su facilidad de manejo, en electrocinética para describir las propiedades del campo en el interior de un conductor se recurre a la noción de diferencia de potencial, también denominada tensión eléctrica porque de ella depende el movimiento de las cargas libres de un punto a otro. El sentido de la corriente eléctrica depende no sólo del signo de la diferencia de potencial, sino también del signo de los elementos portadores de carga o cargas móviles presentes en el conductor.

En un conductor metálico los portadores de carga son los electrones (-), por lo que su desplazamiento se producirá del extremo del conductor a menor potencial hacia el extremo a mayor potencial, o en términos de signos desde el polo negativo hacia el positivo. En una disolución salina los portadores de carga son iones tanto positivos como negativos; cuando se somete dicha disolución a una diferencia de potencial constante, como la producida entre los bornes de una pila, se generarán movimientos de carga de sentidos opuestos; las cargas positivas se desplazarán por la disolución del extremo de mayor potencial al de menor potencial, o lo que es lo mismo, del polo positivo de la pila al polo negativo, y las negativas en sentido contrario. Algo semejante sucede en un medio gaseoso ionizado como el que se produce en el interior de un tubo fluorescente o de neón sometido a una diferencia de potencial intensa.

Benjamin Franklin fue el primero en asignar un sentido de circulación a la corriente eléctrica en los conductores metálicos. Él supuso que era la electricidad positiva la que, como un fluido sutil, se desplazaba por el interior del conductor. Según dicha suposición, la corriente eléctrica circularía del polo positivo al negativo. Más de un siglo después la moderna teoría atómica revelaba que los electrones son los portadores de carga en los metales, de modo que el sentido real de la corriente resulta ser justamente el opuesto al avanzado por Franklin. Por razones históricas y dado que en la electrocinética el sentido de circulación de la corriente no tiene mayor trascendencia, se sigue aceptando como sentido convencional el postulado por Franklin. Sin embargo, en otras partes de la física, como la electrónica, la distinción entre ambos resulta importante.

La intensidad de la corriente eléctrica

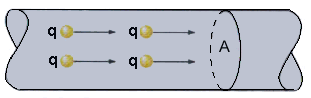
Junto a la idea de movimiento de partículas, la noción de corriente eléctrica lleva asociada la de transporte de carga eléctrica de un punto a otro. La importancia de dicho transporte en términos de cantidad se expresa mediante la magnitud intensidad de corriente eléctrica que se define como la carga total que circula por el conductor en la unidad de tiempo. En forma de ecuación se puede escribir como:

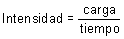
La unidad de intensidad de corriente en el SI recibe el nombre de ampere (A) y equivale a un transporte de carga que se produzca a razón de 1 coulomb (C) en cada segundo (s), 1 A = 1 C/s.

En un metal, en donde la corriente eléctrica es debida únicamente al movimiento de electrones, sólo el transporte de carga negativa contribuye al valor de la intensidad. En las disoluciones iónicas, al ser conducida la corriente tanto por iones positivos como negativos, se produce una doble contribución de ambos tipos de carga a la intensidad de corriente eléctrica.

LA LEY DE OHM

Diferencia de potencial e intensidad de corriente

En un conductor el movimiento de cargas eléctricas es consecuencia de la existencia de una tensión eléctrica entre sus extremos. Por ello la intensidad de corriente que circula por el conductor y la tensión o diferencia de potencial deben estar relacionadas. Otros fenómenos de la física presentan una cierta semejanza con la conducción eléctrica; así el flujo de calor entre dos puntos depende de la diferencia de temperaturas entre ellos y la velocidad de caída de un cuerpo por un plano inclinado es función de la diferencia de alturas.

Ese tipo de analogías, y en particular la relativa a la conducción del calor, sirvió de punto de partida al físico alemán Georg Simon Ohm (1787-1854) para investigar la conducción eléctrica en los metales. En 1826 llegó a establecer que en los conductores metálicos el cociente entre la diferencia de potencial entre sus extremos y la intensidad de corriente que lo atraviesa es una cantidad constante, o en otros términos, que ambas magnitudes son directamente proporcionales. Esta relación de proporcionalidad directa entre tensión e intensidad recibe el nombre de ley de Ohm.

Representando, como es habitual en electrocinética, la tensión eléctrica por V y no por V, la ley de Ohm se puede escribir en la forma:

I = G · V (10.2)

donde G es una constante característica de cada conductor que recibe el nombre de conductancia.

Curva característica de un conductor. Concepto de resistencia

Se denomina curva característica I-V de un conductor a la línea que se obtiene cuando se representa gráficamente la variación de la intensidad de corriente I que atraviesa un conductor con la diferencia de potencial o tensión V aplicada entre sus extremos. Su forma es característica de cada conductor, de ahí su nombre.

La determinación experimental de una curva característica se efectúa mediante un montaje que permita aplicar a los extremos de un conductor cualquiera una tensión variable y que a la vez haga posible la medida tanto de la tensión aplicada como de la intensidad de corriente que constituye la respuesta del conductor. Algunas curvas características I-V son lineales, lo que equivale a decir que en sus conductores correspondientes ambas magnitudes eléctricas son directamente proporcionales. Esto es lo que viene a establecer la ley de Ohm para los conductores metálicos.

En la curva característica I-V de un conductor metálico la pendiente de la gráfica coincide con la constante de proporcionalidad G que, de acuerdo con su definición, constituye una medida de la aptitud para la conducción eléctrica del cuerpo considerado. Cuanto mayor sea G, mayor será la inclinación de la característica I-V y, por tanto, mayor la intensidad que circulará por el conductor para una misma diferencia de potencial.

La inversa de la conductancia G se denomina resistencia eléctrica y se representa por la letra R:

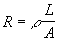
Desde un punto de vista físico, la resistencia R de un conductor constituye una medida de la oposición que presenta éste al paso de la corriente eléctrica. En los metales los electrones han de moverse a través de los átomos de la estructura cristalina del propio metal. Tales obstáculos al movimiento libre de las cargas contribuyen, en su conjunto, al valor de la resistencia R.

La expresión (10.2) puede escribirse, haciendo intervenir a la resistencia, en la forma:

V = I · R (10.3)

que constituye la expresión más conocida de la ley de Ohm.

A partir de la ecuación anterior se define el ohm ( 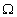) como unidad de resistencia eléctrica en la forma:

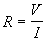
El hecho experimentalmente observado de que no todos los conductores posean características I-V rectilíneas indica que no todos cumplen la ley de Ohm. Es ésta, por tanto, una ley de carácter restringido que sólo puede aplicarse a cierto tipo de conductores llamados óhmicos. En los no óhmicos la resistencia no tiene un valor constante, sino que éste depende de la tensión que se aplique entre los extremos del conductor.

Resistividad y conductividad

Experimentos con hilos metálicos de diferentes longitudes y grosores llevaron a Ohm a establecer el concepto de resistencia al observar que la intensidad I de corriente era inversamente proporcional a la longitud l del conductor y directamente proporcional a su sección S o grosor. Cuando este descubrimiento se combina con la relación de proporcionalidad inversa entre R e I que establece su famosa ley, resulta la relación:

donde 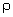es una constante característica del tipo de metal que constituye el hilo conductor considerado. Dicha constante se denomina resistividad y equivale a una resistencia específica referida a una longitud y sección unidad. Se expresa en ohms x metro (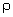 · m). La inversa de la resistividad recibe el nombre de conductividad y se representa por la letra 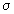( 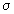= 1/r). Se expresa en 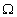-1 · m-1 y caracteriza el comportamiento de un material como conductor eléctrico. En los metales, 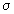toma valores del orden de 107 -1 · m-1 y en los aisladores típicos como el vidrio o la parafina alcanza 10-14 en el primer material y 10-17 -1 · m-1 en el segundo. Los materiales semiconductores presentan valores de intermedios.

El significado energético de la ley de Ohm

Dado que la diferencia de potencial V constituye una energía por unidad de carga, la ley de Ohm puede ser interpretada en términos de energía. Las colisiones de los electrones en los metales con los nudos de la red cristalina llevan consigo una disipación de energía eléctrica. Dicho fenómeno es el responsable de la pérdida o caída de potencial V que se detecta, en mayor o menor medida, entre los extremos de un conductor, e indica que cada unidad de carga pierde energía al pasar de uno a otro punto a raz6oacute;n de V julios por cada coulom0b de carga que lo atraviese.

Si se aplica el principio general de conservación de la energía a los fenómenos eléctricos, la ley de Ohm, definida por la expresión (10.3), puede ser considerada como una ecuación de conservación en donde el primer miembro representa la energía perdida en el circuito por cada unidad de carga en movimiento y el segundo la energía cedida al exterior por cada coulomb que circula entre los puntos considerados.

ELEMENTOS DE UN CIRCUITO

Generadores eléctricos

El movimiento de los electrones por un conductor metálico como consecuencia de una diferencia de potencial entre sus extremos puede compararse con el flujo de agua entre depósitos situados a diferente altura y conectados mediante una tubería. Cuando se llena el depósito superior el agua desciende, pero dicho movimiento dura sólo en tanto se mantiene una diferencia entre los niveles de agua en ambos depósitos. Para mantener el agua en continua circulación es necesario intercalar una bomba que eleve de nuevo el agua desde el depósito inferior al superior. El papel de la bomba en dicho circuito hidráulico es el de comunicar a la masa de agua que lo atraviesa la energía suficiente como para salvar la diferencia de altura entre los dos depósitos, lo que equivale de hecho a mantener constante la diferencia de niveles del agua entre ambos depósitos aun a pesar del flujo continuo que los atraviese.

Para mantener una corriente eléctrica en el interior de un conductor es preciso que exista una diferencia de potencial constante entre sus extremos; hace falta, pues, un dispositivo que juegue un papel análogo al de la bomba en el circuito hidráulico. Dicho dispositivo recibe el nombre de generador. Una asociación de conductores con un generador constituye un circuito eléctrico en donde puede tener lugar un movimiento continuado de cargas. El generador mantiene constante la diferencia de potencial entre dos puntos del circuito, o dicho en otros términos, genera un campo eléctrico en el conductor que es el responsable de la corriente.

Fuerza electromotriz de un generador

La fuerza electromotriz es la magnitud que caracteriza el comportamiento del generador en un circuito eléctrico. En el caso de una bomba hidráulica la potencia mecánica representa la energía que suministra al circuito por unidad de tiempo. En los circuitos eléctricos se define la fuerza electromotriz de un generador y se representa mediante la letra e, como la energía que cede el generador al circuito por cada unidad de carga que lo atraviesa y que se invierte en incrementar su energía potencial eléctrica. Cada carga al pasar por el generador recibe una dosis de energía que podrá gastar después en su recorrido a lo largo del circuito.

Con frecuencia, se emplean las iniciales f.e.m. para designar esta magnitud, que siendo una energía se la denomina impropiamente fuerza. Según su definición la f.e.m. se expresará en unidades de energía partido por unidades de carga. Este es también el caso de las magnitudes potencial y diferencia de potencial. Por tal motivo su unidad en el SI es el voltio.

Tipos de generadores

El tipo de generadores más conocido es el generador químico, al cual pertenece la pila eléctrica o pila seca. Transforma energía producida en ciertas reacciones químicas en energía eléctrica capaz de mantener una diferencia de potencial constante entre sus polos o bornes. Una pila cinc-carbón, como las que se emplean para alimentar un aparato de radio portátil, está formada por dos elementos o electrodos de diferentes sustancias. Uno es de cinc y tiene forma de envoltura cilíndrica, el otro es una barrita de carbón. Entre ambos existe una pasta intermedia o electrolito que contribuye al proceso de generación de tensión. La reacción química que se produce en el electrodo de cinc libera electrones, con lo que éste se convierte en un polo negativo (cátodo); la que se produce en el electrodo de carbón da lugar a una disminución de electrones, resultando de signo positivo (ánodo). La tensión producida por una pila es constante y al aplicarla sobre un circuito eléctrico produce una corriente continua. Este tipo de corriente se caracteriza porque el sentido del movimiento de los portadores de carga se mantiene constante.

La pila de combustible es otro tipo de generador químico de uso frecuente en el suministro de energía eléctrica a naves espaciales. Recibe este nombre porque las sustancias que participan en las correspondientes reacciones químicas son, en parte, introducidas desde el exterior como si de un combustible se tratara. Una pila de combustible típica es la que se basa en las reacciones hidrógeno- oxígeno que se producen con pérdida de electrones en un electrodo y ganancia en el otro, dando lugar a una diferencia de potencial capaz de producir una corriente eléctrica exterior.

Un termopar es un generador termoeléctrico que transforma calor en electricidad. Se produce cuando dos hilos conductores unidos entre sí por sus extremos respectivos se someten a una diferencia de temperatura, sumergiendo una de las soldaduras en hielo fundente y aplicando a la otra la llama de un mechero. Entre ambos puntos se genera una diferencia de potencial que aumenta con la temperatura y puede detectarse con un aparato de medidas eléctricas. Dicho efecto generador de electricidad conocido como efecto Seebeck se emplea principalmente en la medida de temperaturas.

La célula fotovoltaica es un generador de tipo fotoeléctrico que transforma la energía lúminosa en energía eléctrica. Se basa en la, capacidad de los semiconductores para conducir la electricidad en un sentido dado, pero no en el opuesto. Al incidir la luz sobre la célula, arranca algunos electrones de sus átomos, electrones que se acumulan en una región determinada a expensas de la pérdida de electrones en la región opuesta.
Al igual que en una pila seca, estas dos regiones constituyen los polos negativo y positivo, respectivamente, de la célula cuya diferencia de potencial se mantendrá constante en tanto no varíe la intensidad luminosa que alcanza su superficie.

El generador electromagnético se basa en el fenómeno de la inducción electromagnética. Cuando un conductor cerrado se hace girar en el seno del campo magnético producido por un imán se genera en su interior una diferencia de potencial capaz de producir una corriente eléctrica. Es el tipo de generador denominado alternador que se emplea en las grandes plantas de producción de energía eléctrica.
En ellas, diferentes formas de energía, cuya naturaleza depende del tipo de central, se invierten en mover grandes bobinas de conductores, haciéndolas girar en el seno de campos magnéticos. De este modo se producen tensiones eléctricas entre sus bornes cuya polaridad positiva/negativa, se invierte alternativamente con el tiempo a razón de cincuenta veces en cada segundo. Cuando esta tensión se aplica a un circuito eléctrico, produce en él una corriente alterna que se caracteriza por una inversión alternativa, con idéntica frecuencia, del sentido del movimiento de los portadores de carga.

VOLTÍMETRO Y AMPERÍMETRO

Son dos aparatos de medidas eléctricas que puede considerarse como galvanómetros modificados. El primero se utiliza para medir diferencias de potencial entre dos puntos cualesquiera y el segundo para medir intensidades. Su presencia en el esquema correspondiente a un circuito eléctrico se representa en la forma -V- y -A- respectivamente.

El galvanómetro, cuyo nombre honra a Galvani, aprovecha el efecto magnético de la corriente eléctrica. Consta, en esencia, de un imán entre cuyos polos se dispone una bobina que puede girar sobre un eje dispuesto perpendicularmente al plano del imán.
Una aguja solidaria con el bastidor de la bobina hace visible, sobre una escala graduada, el posible movimiento de aquélla. Este movimiento se halla impedido en ausencia de corriente por dos muelles recuperadores o resortes en espiral. Cuando se hace pasar una corriente por la bobina, aparece una fuerza magnética entre la bobina y el imán que desvía la aguja de su posición inicial tanto más cuanto mayor es la intensidad de corriente.

Un amperímetro consiste, básicamente, en un galvanómetro con un shunt o resistencia en paralelo con la bobina, de magnitud lo suficientemente pequeña como para conseguir que prácticamente toda, la corriente se desvíe por ella y que el aparato de Medida perturbe lo menos posible las condiciones del circuito. Los amperímetros se conectan en serie con el circuito, es decir, se intercalan entre los puntos en donde se desea medir la intensidad.

Un voltímetro viene a ser un galvanómetro con una importante resistencia asociada en serie con él. El conjunto se conecta en paralelo o derivación entre los puntos cuya diferencia de potencial se desea medir. Si la resistencia total del voltímetro es mucho mayor que la del circuito, entre tales puntos la corriente se derivará en su mayor parte por el tramo que ofrece menor resistencia a su paso y sólo una fracción de ella atravesará el voltímetro. Con ello se logra que la perturbación que introduce en el circuito el aparato de medida sea despreciable.

A menudo, estos dos dispositivos y el ohmetro están incluidos en un dispositivo llamado Multímetro, que se conecta según el uso de cada uno de ellos. Actualmente se pueden encontrar multímetros tanto digitales como analógicos. Generalmente los digitales son más exactos (y más caros) que los analógicos.

Polímetro Analógico

Polímetro Digital

LEYES DE KIRCHHOFF

Existen dos reglas, llamadas Leyes de Kirchhoff, que se aplican a cualquier circuito en estado estacionario:

1. La suma algebraica de las variaciones de potencial a lo largo de cualquier bucle o malla del circuito debe ser igual a 0.

2. En un punto o nudo de ramificación de un circuito en donde puede dividirse la corriente, la suma de las corrientes que entran en el nudo debe ser igual a la suma de las corrientes que salen del mismo.

La regla 1, llamada Regla de las mallas, se deduce a partir del simple hecho de que en el estado estacionario la diferencia de potencial entre dos puntos cualesquiera es constante. En estado estacionario, el campo eléctrico en cualquier punto (fuera de una fuente de fem) es debido a la carga acumulada sobre las superficies de los bornes de la batería, resistencias, cables, u otros elementos del circuito. Como el campo eléctrico es conservativo, existe una función potencial en cualquier punto del espacio (excepto en el interior de una fuente de fem). Según nos desplazamos a lo largo de la malla y se ha llegado al punto desde el que se comenzó, la variación neta del potencial debe ser igual a cero. Esta regla es una consecuencia directa del principio de conservación de la energía.

La segunda regla de Kirchhoff, Regla de los nudos, se deduce de la conservación de la carga. Esta regla es necesaria para circuitos de múltiples mallas que contienen puntos en los que la corriente puede dividirse. Como en estado estacionario no hay posterior acumulación de carga eléctrica en ningún punto del circuito, la cantidad de carga que entra en un punto, debe ser igual a la que sale de dicho punto.

Ej: Dado el siguiente circuito.

Al escribir la primera ley, debemos considerar aquellas corrientes que salen de un nudo como positivas y las que llegan como negativas. La primera ley expresa la conservación de la carga porque, como las cargas no se acumulan en un nudo, el número de cargas que llegan a un nudo en un cierto tiempo debe ser igual al número de cargas que salen en el mismo tiempo.

Al aplicar la segunda ley debemos tomar en cuenta las siguientes reglas. Una caída de potencial a través de una resistencia es positiva o negativa según que recorramos el circuito en el sentido de la corriente o en sentido opuesto. Cuando pasamos a través de una fem, tomamos la diferencia de potencial como negativa o positiva dependiendo de que la atravesemos en el sentido en que actúa la fem. La segunda ley expresa la conservación de energía, ya que la variación neta de energía de una carga después de haber recorrido un camino cerrado debe ser 0.

Aplicamos estas leyes para este circuito.

La primera ley aplicada a los nudos A, B y C da:

Nudo A: -I1+I2+I3=0

Nudo B: -I3+I4+I5=0

Nudo C: -I2 -I4+I6=0

La segunda ley aplicada a los recorridos 1,2 y 3 da:

Recorrido 1: -R2I2+R3I3+R4I4-Ve2=0

Recorrido 2: R5I5-R6I6-R4I4=0

Recorrido 3: R1I1+R2I2+R6I6-Ve1+Ve2=0

Estas 6 ecuaciones son suficientes para determinar las seis corrientes en la red.

RESISTENCIA EQUIVALENTE (Re)

Un circuito eléctrico está formado por la asociación de una serie de elementos conductores que hacen posible el mantenimiento por su interior de una corriente eléctrica. Si los generadores producen una diferencia de potencial constante entre sus bornes o polos, la corriente producida será continua. Tal es el caso de las pilas y de las baterías.

En los circuitos de corriente continua pueden distinguirse básicamente dos tipos de elementos, los generadores y los receptores. Los primeros aportan al circuito la energía necesaria para mantener la corriente eléctrica, los segundos consumen energía eléctrica y, o bien la disipan en forma de calor, como es el caso de las resistencias, o bien la convierten en otra forma de energía, como sucede en los motores. Una pila en un circuito eléctrico se representa mediante el símbo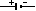lo que refleja la polaridad del generador. Una resistencia se representa por el símbolo .

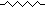Para simplificar el estudio, se supone que las magnitudes o parámetros característicos de estos elementos se concentran en los puntos del circuito donde se representan. Así, la resistencia de los cables de conexión o se desprecia o se supone concentrada en un punto como si se tratara de un elemento de circuito más.

El estudio cuantitativo de los circuitos eléctricos de corriente continua se efectúa como una aplicación de dos principios básicos:

El principio de conservación de la energía referido a la unidad de carga eléctrica, según el cual en todo el circuito, o en cualquier tramo de él, la energía que pierde la corriente eléctrica es igual a la energía cedida por el circuito al exterior. Es, en esencia, la ley de Ohm generalizada e interpretada como balance de energías.

El principio de no acumulación de cargas, que indica que las cargas no pueden acumularse. Eso significa que si no hay bifurcaciones, la intensidad de corriente es la misma en todo el circuito, y si las hay, la intensidad de corriente que entra en un nudo o punto de bifurcación ha de ser igual a la suma de las que salen de él.

Tales principios se conocen también como leyes de Kirchoff.

Asociación de resistencias

Existen dos modos fundamentales de conectar o asociar las resistencias entre sí, en serie y en paralelo o derivación. En la asociación en serie las resistencias se conectan una tras otra de modo que por todas ellas pasa la misma intensidad de corriente. En la asociación en paralelo la conexión se efectúa uniendo los dos extremos de cada una de ellas a un mismo par de puntos. En este caso la diferencia de potencial entre los extremos de cualquiera de las resistencias asociadas es la misma, pero, de acuerdo con el principio de no acumulación de cargas, la intensidad total que llega al nudo o punto de bifurcación se reparte entre ellas.

Se denomina resistencia equivalente de una asociación de resistencias a aquella resistencia única por la que podría sustituirse la asociación sin alterar la intensidad que circula por el circuito. En el caso de una asociación en serie de tres resistencias, la fórmula de la resistencia equivalente Re se obtiene como sigue. De acuerdo con la ley de Ohm aplicada a cada una de ellas, se tiene:

V1 = I · R1 ; V2 = I · R2 ; V3 = I · R3

donde V1, V2 y V3 son las tensiones entre sus extremos respectivos e I la intensidad de corriente que las atraviesa, igual para todas ellas.

De acuerdo con el principio de conservación de energía referido a la unidad de carga, la cantidad total de energía que pierde la unidad de carga al atravesar las tres resistencias será igual a la suma de las cantidades que pierde en cada resistencia, es decir:

V = V1 + V2 + V3 = IR1 + IR2 + IR3 =
= I · (R1 + R2 + R3)

Si la ley de Ohm se aplica a la asociación en su conjunto, se tiene

V = I · Re

Comparando ambas ecuaciones resulta:

Ecuación que puede generalizarse a cualquier número de resistencias.

Si la asociación fuera en paralelo, al llegar al nudo la corriente se reparte entre las diferentes resistencias y, de acuerdo con el principio de no acumulación de cargas, se cumplirá, en este caso, la relación

I = I1 + I2 + I3

con

V1 = V2 = V3 = V

Aplicando la ley de Ohm a cada resistencia, resulta ahora:

V = I1 · R1 ; V = I2 · R2 ; V = I3 · R3

Para la asociación en su conjunto se tendrá:

V = I · Re

Si se sustituyen los valores de I, I1, I2 e I3 en la ecuación de las intensidades se obtiene:

es decir:

En este caso es la suma de los inversos la que da lugar, no a la resistencia equivalente, sino a su inverso. Por tal motivo en este tipo de asociación el valor de la Re, resulta ser inferior al de la más pequeña de las resistencias asociadas.

Análisis de circuitos

En el estudio del comportamiento de cualquiera de las partes o de los elementos de un circuito, se precisa conocer cuál es la intensidad de corriente que circula por él. La determinación de la intensidad o intensidades de corriente que circulan por todos y cada uno de los elementos de un circuito dado recibe el nombre de análisis de circuito.

En el caso de circuitos simples con un solo generador, o con varios asociados en serie, es posible llevar a término el análisis de circuitos aplicando de forma general los principios anteriormente considerados, así como las fórmulas de asociación de resistencias. Sin embargo, cuando existen varios generadores distribuidos por diferentes bifurcaciones o ramas el problema del análisis se complica y es preciso recurrir a procedimientos más potentes y también más laboriosos.

LEY DE JOULE

La ley de Joule permite calcular la energía disipada en forma de calor en un conductor. Su expresión matemática es Q = I2 · R · t, siendo R la resistencia en ohms, I la intensidad de corriente en amperios y t el tiempo en segundos.

Para elevar la temperatura del agua en 1 ºC se necesitan 4,2 J por cada gramo. Se trata de determinar, aplicando la ley de Joule, el valor de la resistencia eléctrica que debe tener un calentador eléctrico para que, conectado a un enchufe de 220 V, sea capaz de elevar la temperatura de un litro de agua de 15 ºC a 80 ºC en cinco minutos.

La energía calorífica necesaria para elevar la temperatura del agua de 15 ºC a 80 ºC será:

Q = 1000 · (80 - 15) · 4,2 = 2,73 · 105 J

pues un litro de agua corresponde a un kilogramo de masa y 4,2 representa el calor en joules por gramo y grado centígrado (calor específico).

Dado que se dispone del valor de la tensión, pero no de la Intensidad, será necesario transformar la ley de Joule de modo que en la fórmula correspondiente aparezca aquélla y no ésta. Recurriendo a la ley de Ohm V = I · R se tiene:

Despejando R y sustituyendo los valores conocidos resulta:

POTENCIA ELÉCTRICA

La energía eléctrica We que suministra un generador al circuito eléctrico depende de la cantidad de carga que lo atraviese. Dado que la fuerza electromotriz de un generador representa la energía que suministra al circuito por cada unidad de carga que lo atraviesa, se podrá escribir:

es decir:

Pero de acuerdo con la definición de intensidad eléctrica, la carga eléctrica q se puede escribir como el producto de la intensidad por el tiempo (10 · 1); luego la energía eléctrica suministrada por el generador al circuito en un tiempo t vendrá dada por la expresión:

La potencia P de un generador representa la energía eléctrica que cede al circuito por unidad de tiempo, es decir:

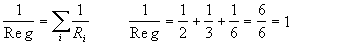
Combinando las anteriores ecuaciones resulta para P la expresión:

Al igual que la potencia mecánica, la potencia eléctrica se expresa en watts (W).

Efectos caloríficos de la corriente eléctrica. Ley de Joule

El calentamiento de los conductores por el paso de la corriente eléctrica fue uno de los primeros efectos observados por los científicos estudiosos de los fenómenos eléctricos, sin embargo, habría de pasar algún tiempo antes de que se conociera la magnitud de tal efecto calorífico y los factores de los que depende. J. P. Joule (1818-1889) se interesó desde joven en la medida de temperaturas de motores eléctricos, lo que le permitió hacia 1840 encontrar la ley que rige la producción de calor por el paso de una corriente eléctrica a través de un conductor.

La ley de Joule establece que la cantidad de calor producida es directamente proporcional a la resistencia R del conductor, al cuadrado de la intensidad de corriente I que lo atraviesa y al tiempo t. Es decir:

Q = I2 · R · t (10.8)

El efecto calorífico, también llamado efecto Joule, puede ser explicado a partir del mecanismo de conducción de los electrones en un metal. La energía disipada en los choques internos aumenta la agitación térmica del material, lo que da lugar a un aumento de la temperatura y a la consiguiente producción del calor. La ley de Joule, por su parte, puede ser enfocada como una consecuencia de la interpretación energética de la ley de Ohm. Si I · R representa la energía disipada por cada unidad de carga, la energía total que se disipa en el conductor en forma de calor, cuando haya sido atravesado por una carga q, será:

Q = q · I · R

Pero dado que q = I · t, se tiene finalmente:

Q = I2 · R · t

que es precisamente la ley de Joule.

La potencia calorífica representa el calor producido en un conductor en la unidad de tiempo. Su expresión se deduce a partir de la ley de Joule en la forma:

Puesto que el calor es una forma de energía, se expresa en joules (J) y la potencia calorífica en watts (W).

Cuando se combinan las ecuaciones (10.9) y (10.3) resulta otra expresión para la potencia eléctrica consumida en un conductor:

P = IR · I = I · V (10.10)

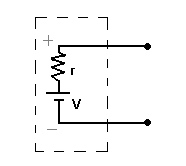
Fuerza electromotriz y diferencia de potencial

La noción de fuerza electromotriz de un generador como energía que comunica el circuito por cada unidad de carga que lo atraviesa, está referida a un generador ideal o puro. En tal caso toda la energía que produce el generador la cede íntegramente al circuito, por lo cual la fuerza electromotriz e coincide exactamente con la diferencia de potencial V constante que mantiene entre sus bornes:

En realidad, una pila, una batería o un alternador son en sí mismos elementos conductores que forman parte del circuito por donde pasa la corriente y en mayor o menor medida oponen, como tales, una cierta resistencia al movimiento de las cargas.

Ello significa que el generador, al formar parte del circuito, se calienta y disipa, por tanto, una cierta cantidad de calor. La idea de balance de energía a la que equivale la interpretación de la ley de Ohm en términos energéticos puede entonces extenderse al caso de un generador con el propósito de encontrar la relación entre e y V en esta nueva situación. Aplicando la conservación de la energía por unidad de carga a los extremos del generador, se tiene:

que en forma de símbolos resulta ser:

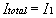
Esta ecuación se conoce como ley de Ohm generalizada a un generador y permite determinar la diferencia de potencial que es capaz de mantener entre sus bornes un generador real, esto es, con resistencia interna r no despreciable.

MÉTODO DE LAS CORRIENTES DE MALLAS

• Se eligen m mallas m = nº de ramas (nº de nudos - 1).

• Se le asigna a cada malla una corriente con un sentido (I1,I2,I3).

• Se construye la matriz de impedancias (en c.c. Z = R).

Donde à Zii : Suma de todas la resistencia de una malla.

Zij : Suma de las resistencia que compartidas por la malla i y la malla j

z > 0 si Ii e Ij tienen el mismo sentido.

z < 0 si Ii e Ij tienen distinto sentido.

• Se construye la matriz de voltajes.

Donde à Vi : Suma de los voltajes V en la malla i.

V > 0 si Ii sale de la fuente de alimentación por el borne +.

V < 0 si Ii entra en la fuente de alimentación por el borne -.

(Se mira el signo de salida de la fuente de alimentación.)

• Resolver

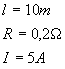
En nuestro caso:

MÉTODO DE LOS VOLTAJES DE NUDOS

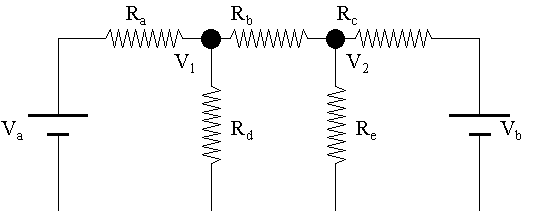
• Se eligen n nudos nº ecuaciones = m = n-1

• Se asigna a cada nudo un potencial vi>0 menos a uno que se le asigna: v=0

• Se construye la matriz de admitancias (en C.C. Y=1/R)

yiiº suma de todas las admitancias del nudo i

yijº suma de las admitancias compartidas entre los nudos i y j

yij < 0 siempre

Ejemplo:

y11=1/Ra+1/Rd+1/Rb, y12=-1/Rb, y21=-1/Rb, y22=1/Rd+1/Rc+1/Re

y13=y31=y23=y32=y33=0

• Se construye la matriz de intensidades

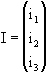
ii= suma de las intensidades aplicadas al nudo i

I>0 si las corrientes entran al nudo

I<0 si las corrientes salen del nudo

Ejemplo:

i1=Va/Ra, i2=Vb/Rc, i3=0

• Se resuelve la ecuación matricial

LA SUPERCONDUCTIVIDAD

La superconductividad es una propiedad que presentan algunos materiales sometidos a ciertas condiciones especiales, de conducir la electricidad sin oponer ninguna resistencia y, por tanto, sin disipar energía por efecto Joule. Aun cuando el fenómeno de la superconductividad fue descubierto por Kamerlingh Onnes en 1911, hasta hace sólo unos años resultaba necesario, para conseguir tal propiedad, someter a ciertos metales a temperaturas próximas al cero absoluto (- 273 ºC).

Investigaciones recientes han conseguido sintetizar materiales de tipo cerámica capaces de convertirse en superconductores a temperaturas mucho más altas. La desenfrenada carrera científica que se ha desatado en este campo permite albergar la esperanza de conseguir, a corto plazo, materiales superconductores a temperaturas muy próximas a la ambiente.

La importancia de este logro científico puede resultar decisiva en un buen número de aplicaciones técnicas. Cabe destacar la posibilidad de fabricar electroimanes a base de superconductores con un coste reducido, lo cual abarataría la construcción de algunos sofisticados aparatos de diagnóstico médico que emplean potentes imanes, facilitaría la producción de la energía del futuro y permitiría construir medios de transporte terrestre ultrarrápidos y económicos basados en la sustentación o levitación magnética. Un tren experimental alemán de estas características ha conseguido una velocidad de 406 km/h. Este tipo de trenes, al desplazarse sin entrar en contacto con el suelo, evitan los efectos indeseables del rozamiento y equivalen a aviones que se muevan en vuelo rasante.

Recibir las novedades por mail

Guardar: