Este estudio comienza con el estudio de la línea de transmisión desde el punto de vista de la teoría de circuitos clásica, pero teniendo en cuenta que, en la línea, las constantes no se encuentran concentradas, sino distribuidas a lo largo de la longitud de la línea.

Para que sea válida la teoría de los circuitos, las constantes deberían ser concentradas, o dicho de otro modo, la longitud de onda l debe ser mayor que las dimensiones del circuito bajo análisis.

En el caso de las líneas de transmisión, por lo general se cumple que la longitud de onda l de la señal es mucho menor que la longitud de la línea de transmisión y por lo tanto, no se pueden considerar a las constantes de la línea como concentradas, sino como distribuidas a lo largo de ella, por lo que la teoría clásica sería in aplicable.

Para salvar este inconveniente, consideramos a la línea de transmisión compuesta por una sucesión de elementos de línea, cada uno de ellos, poseyendo una longitud infinitesimal dl; para cada uno de estos elementos será válida la aplicación de la teoría de los circuitos, puesto que l>>dl.

En conclusión, ¿existe físicamente una línea de transmisión? Pues diremos que básicamente se trata de dos conductores próximos entre sí, cuya finalidad es la de guiar la onda electromagnética que se propaga de modo transversal electro magnético (TEM); los vectores campo eléctrico E y campo magnético H son perpendiculares entre sí y perpendiculares a la dirección de propagación, es decir a los conductores de la línea. La onda electromagnética, en general de alta frecuencia, desde un generador (un transmisor de alta frecuencia) hasta una carga (generalmente una antena).

Análisis de una línea de transmisión

El siguiente análisis es independiente del tipo de línea, que puede ser: bifilar, coaxil, de cintas paralelas o micro strip. Los conductores que forman la línea se caracterizan por poseer:

1. Una resistencia a la corriente continua y otra resistencia variable con la frecuencia, debido al efecto "pelicular" por el cual la corriente circula por la superficie de l conductor y no por el centro. Ambas resistencias en conjunto definen la Resistencia distribuida medida en W/metro

2. Además, en alta frecuencia, los conductores de la línea se encuentran concatenados por un campo magnético variable, lo que da lugar a una inductancia distribuida.

3. Por otro lado, entre los dos conductores que forman la línea existe una diferencia de potencial que da origen a un campo eléctrico; por este motivo aparece una capacidad distribuida a lo largo de la línea.

4. Por último, puesto que el dieléctrico no es perfecto, presenta componentes de pérdida en paralelo con la línea caracterizando así una conductancia distribuida.

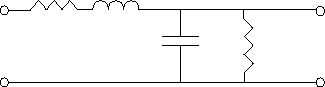
Todos estas características definen al elemento de línea de longitud Dx, que ya habíamos definido. Así, cada elemento de línea de línea Dx estará compuesto por:

1. R = resistencia por unidad de longitud.

2. L = inductancia por unidad de longitud.

3. C = capacidad por unidad de longitud.

4. G = conductancia por unidad de longitud.

Adaptación de Impedancias

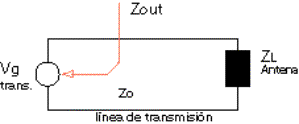
Cuando se conecta un transmisor de radiofrecuencia a una línea de transmisión, siempre se busca que la impedancia característica de la línea, sea igual a la impedancia de salida del transmisor, para lograr así la máxima transferencia de potencia. Lo mismo sucede cuando se desea conectar la antena (carga)  a la línea. En caso de que las impedancias de línea y carga sean distintas, parte de la energía entregada por el transmisor, "rebotará" en la antena, volviendo como una onda reflejada. Es por eso que ahora analizaremos distintos métodos prácticos para lograr adaptar la impedancia entre la línea de transmisión y la antena.

El método de adaptación de pende de si la carga es real pura (R) o compleja (R + jX).

Transformador de cuarto de onda. Carga real pura.

Dependiendo de su longitud, una línea de transmisión con una cierta carga (real o imaginaria) puede representar una impedancia diferente para el generador. Esto se calcula con la siguiente fórmula:

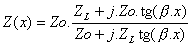
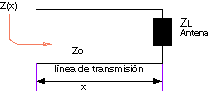
En la imagen de arriba vemos que dependiendo del largo x, varía la Z de entrada Z(x) o Ze. El objetivo del primer método consiste en construir un tramo de línea de longitud igual a l/4 (un cuarto de onda) de una impedancia tal que a su entrada presente una Ze igual al de la línea de transmisión que se va a emplear: Ze = Zo.  

Si consideramos:

1. x = l/4

2. ZL = RL

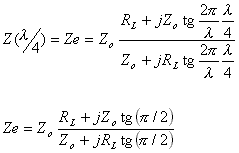
Llegamos a una indeterminación, la cual si es salvada nos lleva a:

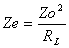
En conclusión: a una distancia igual a l/4 de la carga, la impedancia de entrada depende tanto de la impedancia característica de la línea como de la resistencia de la carga.

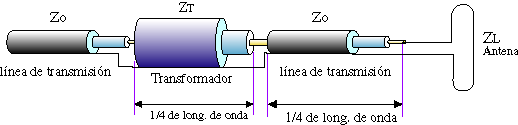
Como es fácil construir una línea de transmisión de una impedancia específica, lo que se hace es calcular que impedancia debería tener una línea de l/4 de longitud conectada directamente a la carga para que represente para la línea de transmisión que se va usar una impedancia idéntica a la de esta. Gráficamente sería lo siguiente:

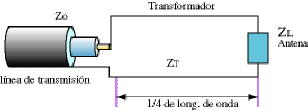
Como vemos, la impedancia del transformador ahora la llamaremos ZT  y es lo que deseamos calcular. Las variables serán ZL, que como es resistiva pura la podemos llamar RL también, y Zo, la impedancia de la línea que usaremos para conectar con el transmisor. Según la fórmula anterior la impedancia del transformador será:

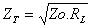
El tramo de línea de un cuarto de onda ZT deberá ser construido, pudiendo ser tanto línea coaxil como bifilar, prefiriéndose la línea bifilar para valores de ZT menores que 120 W por razones constructivas.

Ejemplo 1: Se requiere adaptar una RL = 200 W a una línea de transmisión coaxil cuya Zo 0 50 W. Emplear un transformador de cuarto de onda.

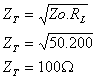
Entonces debemos construir una línea de 100 W, que puede ser coaxil, por tener menos de 120 W. Como hemos visto, la impedancia característica de la línea coaxil se calcula:

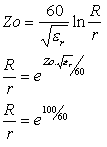
En el ejemplo hemos elegido un dieléctrico de aire con lo que la constante dieléctrica relativa er vale 1. Noten también que si bien en la fórmula de cálculo de la impedancia de la línea dice Zo, en realidad estamos calculando la impedancia característica del tramo de ZT, es decir, el transformador; sucede que siempre se designa como Zo a cualquier impedancia característica.

Uso de dos tramos de cuarto de onda

En ocasiones, puede ser más práctico armar el transformador con línea coaxil en lugar de bifilar debido a las menores pérdidas que tiene la primera. Para ello se conecta la antena con un tramo de la línea de transmisión que se va a usar pero de una longitud de un cuarto de onda, con lo que la impedancia que tendremos a la entrada de esta se podrá calcular fácilmente mediante la fórmula:

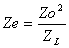
Ahora Ze es como si fuera nuestra carga, por lo que hacemos ZL = Ze y realizamos el cálculo como antes.

Ejemplo 2: Se requiere conectar una antena de ZL = 1000 W a una línea coaxil cuya Zo = 50 W. Diseñar, sobre la base de un transformador de l/4 un sistema de adaptación práctico.

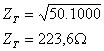
Como ZT es mayor que 120 W, no se puede implementar con coaxil. Entonces conecto a la antena, un tramo de l/4 de línea coaxil de 50 W (la que voy a utilizar para llegar hasta el generador). La impedancia a la salida de este tramo será:

Ahora nuestra impedancia de carga ZL = 2,5 W, con lo que ahora calculamos el transformador de cuarto de onda que debemos construir:

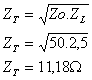
Ahora, una impedancia de 11,18 W es realizable con coaxil.

Desventajas del método: A frecuencias muy bajas tiene gran tamaño y bajo ancho de banda.

Adaptación de cargas complejas

Ahora trataremos la adaptación de cargas complejas, es decir, del tipo Z=R+jX.

Si tenemos una carga compleja, podemos asegurar que a una distancia x, hacia el generador, la carga variará y se comportará como real. En ese punto (en que tenemos una carga real) podemos aplicar los métodos de adaptación antes explicados.

Para adaptar cargas complejas se utiliza el diagrama de Smith. Pueden bajar uno haciendo click aquí. El diagrama de Smith consiste en una serie de circunferencias cada vez mayores donde cada una de ellas representa la Resistencia o la Conductancia (es indistinto). A su vez, estas circunferencias están cruzadas por otras arcos de circunferencia que representan la Reactancia o la Susceptancia.

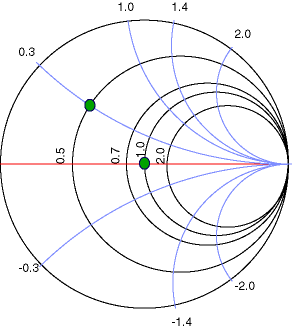
En la imagen podemos ver las circunferencias negras que representan la Resistencia o Conductancia (parte Real) y los arcos de circunferencia celestes representan la parte imaginaria; de la línea roja hacia arriba, es la parte imaginaria positiva y hacia abajo la negativa.

Si trabajamos con Admitancias, las parte superior será la componente capacitiva y la inferior la inductiva. Si trabajamos con Impedancias, será al revés.

Vemos también que se ha marcado, con un círculo verde, el punto en donde la circunferencia de radio=1 corta a la horizontal roja; este punto es el centro del diagrama y nos será de utilidad más adelante.

Cálculo de la Impedancia normalizada

La impedancia normalizada es la que marcamos en el diagrama de Smith. Supongamos que nuestra carga tiene un valor de ZL=50+j30 W y el valor de la impedancia característica de la línea de transmisión es de Zo=100 W. La impedancia normalizada, zl, se calcula:

zl=ZL/Zo

zl=0,5+j0,3

Y vemos que este valor es el que marcamos en el gráfico con otro círculo verde.

Ahora, si trazamos una circunferencia con centro en 1 (centro del diagrama) y con el radio de zl, cualquier impedancia que se encuentre sobre la circunferencia tendrá el mismo ROE (relación de onda estacionaria). A estas circunferencias, con centro en 1, se las llama "de ROE constante". Si nosotros nos "movemos" desde la impedancia de carga, por la circunferencia de ROE constante correspondiente, equivale a "acercarse" al generador (en sentido horario). Si nos movemos en sentido antihorario, nos alejamos del generador.

Si bajan el archivo del diagrama de Smith, verán que alrededor del gráfico hay una escala que dice Wavelength towards the generator y Wavelength towards the load y que significa: distancia en longitudes de onda hacia el generador y hacia la carga, respectivamente.

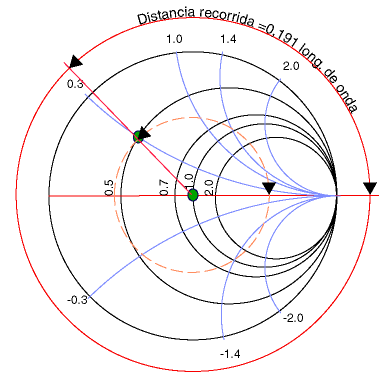
Para convertir una carga compleja en Real pura, debemos girar hacia el generador hasta la línea horizontal y luego medir la distancia en longitudes de onda.

La cuenta que hay que hacer para sacar la distancia es: 0,25-0,059=0,191 longitudes de onda, según la escala de longitudes de onda que figura en el diagrama (no se muestra en la imagen).

Es decir que a una distancia de 0,191 longitudes de onda de la antena, la impedancia es Real pura. El valor normalizado lo leemos de las circunferencias de Resistencia, por ejemplo, z=2 ohms. Este es el valor de la impedancia normalizada; la impedancia real sería ese valor multiplicado por la impedancia de la línea:

Z=z . Zo

Z= 20 W

A partir de acá se procede como un caso de carga real pura.

Recibir las novedades por mail

Guardar: